Day 6: Matrix Maths and PyTorch Tensor.

Review the Matrix maths needed with PyTorch Tensor to understand Neural Networks.

By Nandeshwar

Jun 06, 2021

PyTorch Vs NumPy

We all know that when we think about multi-dimensional matrices and linear algebra, the standard library is NumPy. It is an amazing library with tightly coupled C language bindings for faster computation. There’s also PyTorch - an open-source deep learning framework developed by Facebook Research.

PyTorch provides its own way of storing arrays just like NumPy which are known as Tensors. So technically array management provided by both the libraries is similar. PyTorch Tensors are similar to the NumPy library.

One major difference is torch Tensors can run on GPUs.
Tensors are also optimized for automatic differentiation.

These are a few of the many reasons why we prefer PyTorch Tensors over NumPy arrays at least for Deep Learning. Show me the code!

How to go through this particular article?
In this article, I have covered many PyTorch Tensor methods used for arithmetic operations. I have not explained any method, because I personally suggest going through there documentation respectively.

Wanna jump right to code, check out complete code on Github.

Working with the Tensor

Initializing the tensor

We can also create tensors based on other existing tensors. The new tensor retains the properties (shape, datatype) of the argument tensor unless explicitly overridden.

Now let us say we explicitly want to create a Tensor of shape (2, 3)

Each of its elements is randomly sampled from a standard Gaussian (normal) distribution with a mean of 0 and a standard deviation of 1.

Similarly, as torch.ones we can also create matrices with torch.zeros.

Here, torch.arange returns a 1-D tensor of size $ \left\lceil \frac{\text{end} - \text{start}}{\text{step}} \right\rceil $ with values from the interval [start, end) taken with common difference step beginning from start.

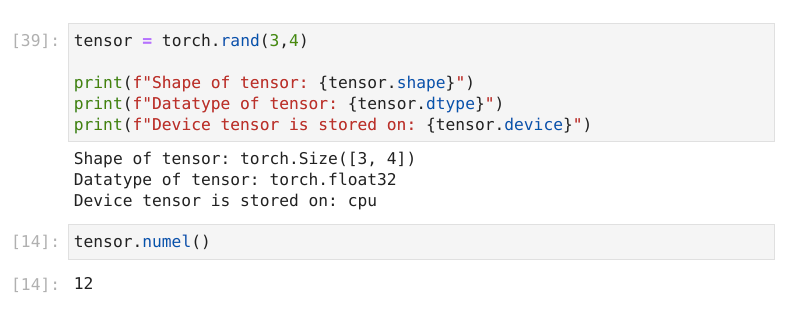
Attributes of a Tensor

Tensor attributes describe their shape, datatype, and the device on which they are stored.

Changing Shapes of Tensor

.shape is an alias for .size(), and was added to more closely match numpy, see #1983

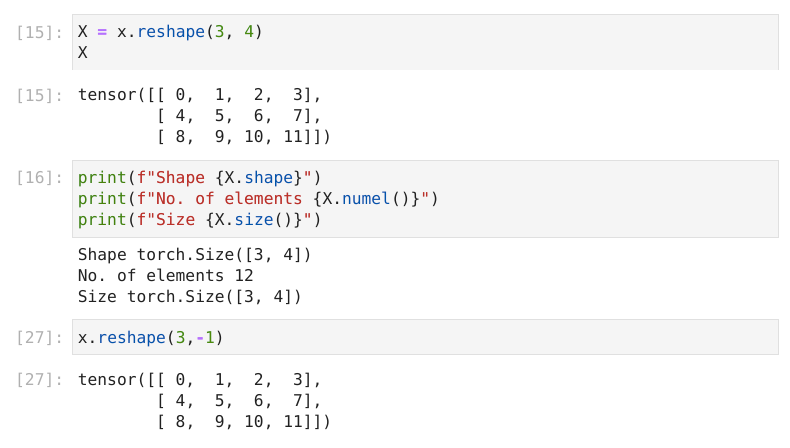
Sometimes we need to change the dimensions of data without actually changing its contents. This is done to make calculations more simple.

For example, there is a vector, which is one-dimensional but needs a matrix, which is two-dimensional. Notice that the content of all three tensors is the same.

Operations on Tensors

Over 100 tensor operations, including arithmetic, linear algebra, matrix manipulation (transposing, indexing, slicing), sampling, and more. Each of these operations can be run on the GPU (at typically higher speeds than on a CPU). If you’re using Colab, allocate a GPU by going to Runtime > Change runtime type > GPU.

By default, tensors are created on the CPU. We need to explicitly move tensors to the GPU using the .to method (after checking for GPU availability). Keep in mind that copying large tensors across devices can be expensive in terms of time and memory!

# We move our tensor to the GPU if available
if torch.cuda.is_available():
    print('GPU found')
    tensor = tensor.to('cuda')
else:
    print('No GPU')

Tensor Arithmetic Operations

All mathematical operations can be easily done on tensors.

Arithmetic operations with different shapes

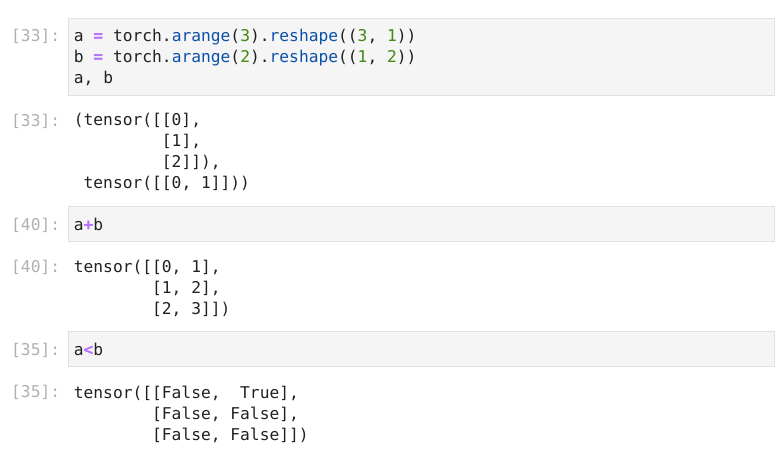
Tensors can be concatenated with each other in either dimension

Specifying axis=1 will reduce the column dimension (axis 1) by summing up elements of all the columns. Thus, the dimension of axis 1 of the input is lost in the output shape.

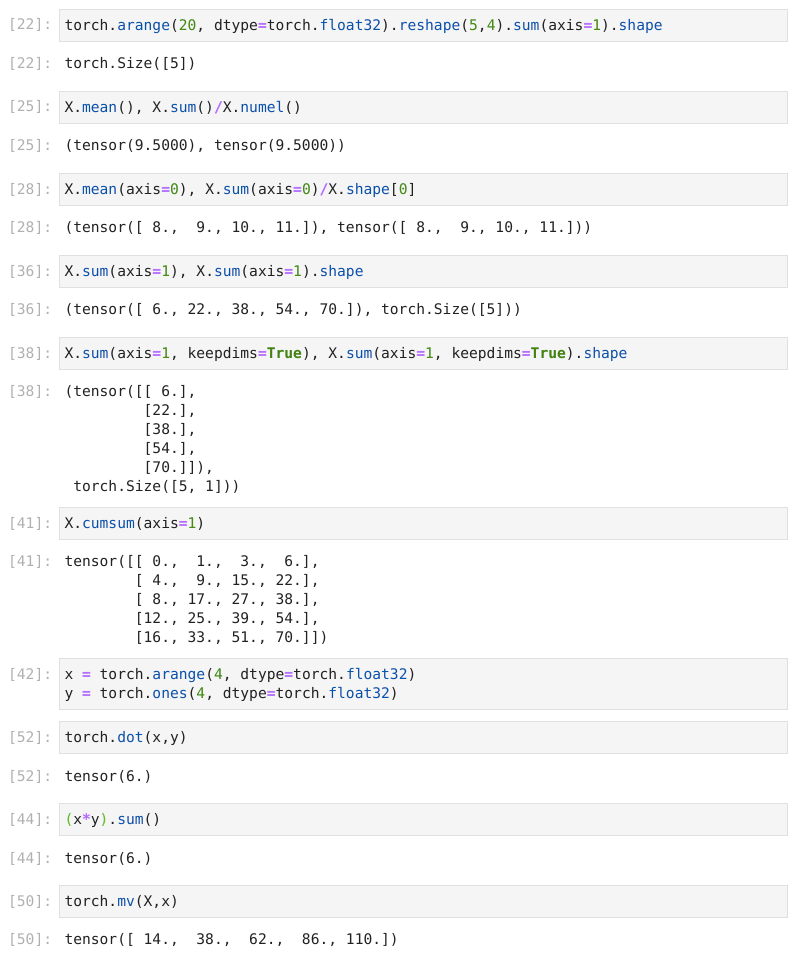
The main interface to store and manipulate data for deep learning is the tensor (nn-dimensional array). It provides a variety of functionalities including basic mathematics operations, broadcasting, indexing, slicing, memory saving, and conversion to other Python objects.

Get the complete code on GitHub.